
パスカルといえば、哲学者・数学者であることで有名ですが、幾何学者(簡単に言うなら図形問題だけを取り扱う学者)としても名高いのです。そして、何よりパスカルが最初に学者デビューを果たしたのも幾何学の分野なのです。
ルーレット。
もはやカジノの代名詞とも言っていいあの道具です。
実は元々幾何学の問題を表す言葉であり、パスカルが付けたものなのです。
一体どういうものなのか、他にパスカルはどのような幾何学の業績があるのか。面白おかしく紹介していきます。
結論から言うなれば、
- デカルトすら嫉妬させた(?)パスカルの定理(神秘的六芒星)
- 自分で開いたコンテストなのに優勝者が居ず、結局自分を優勝としてしまったサイクロイド問題(ルーレット問題)
です。
パスカルの定理から説明していきましょう。
下記クリックで好きな項目に移動
パスカルの数学者としての業績
1・パスカルの定理
パスカルの定理とは「円に内接する六角形ABCDEFの底辺を延長した直線の交点をP、Q、Rとするとその3点が一直線上になる」というものです。

分からないのは字面だけ追っているからです。ちょっと手を動かしてみましょう。
というわけで、皆さん、紙とペンをご用意ください。準備できたら下の記事を読んで、その通りにやってみてください。
Are you ready?(パスカルの定理をやってみよう!)
1・紙に円を描く
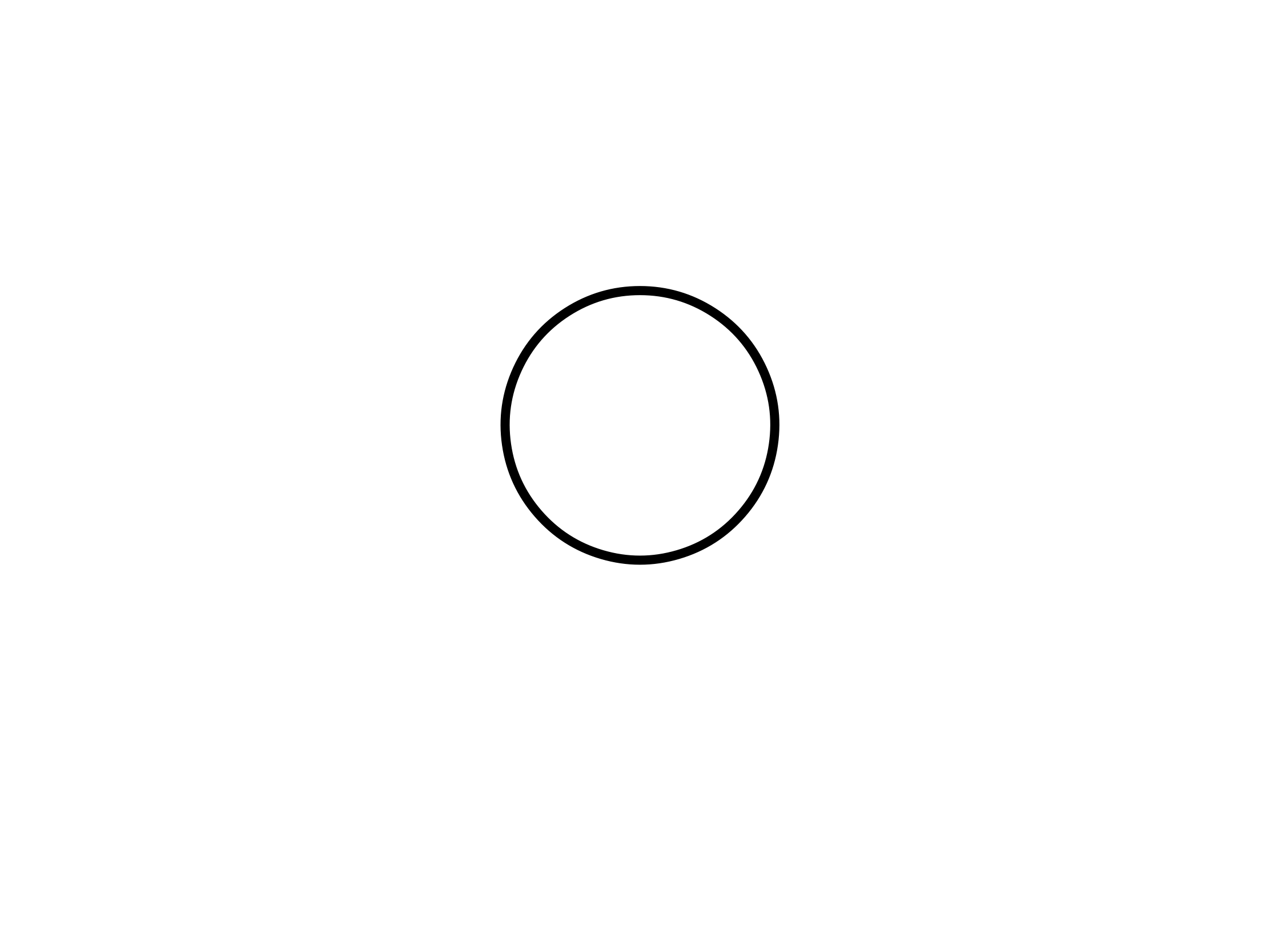
2・こんな風に6個点を打って、それぞれをABCDEFとする
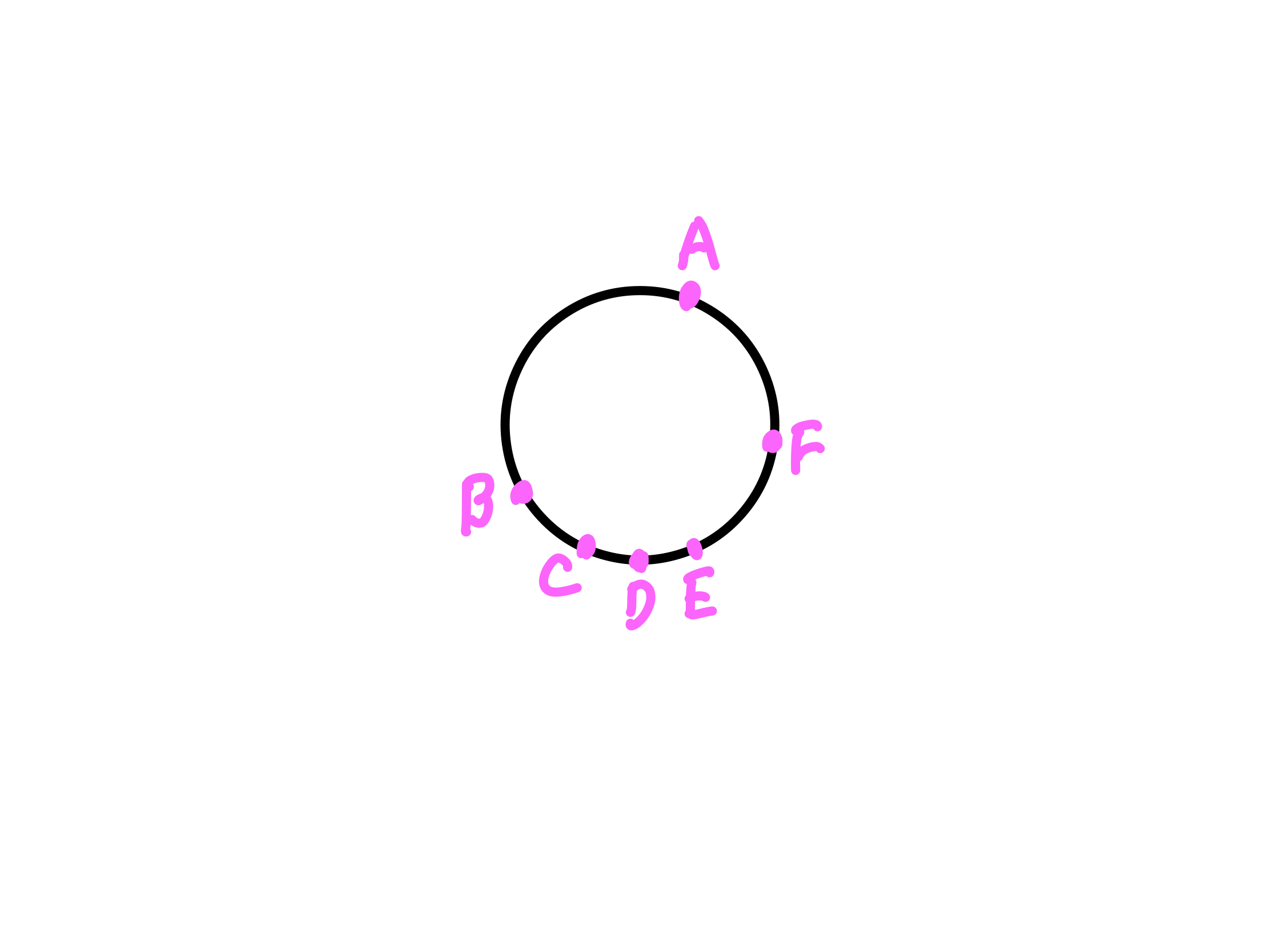
3・線ABと線DEを延長して、ぶつかるところを点Pとする
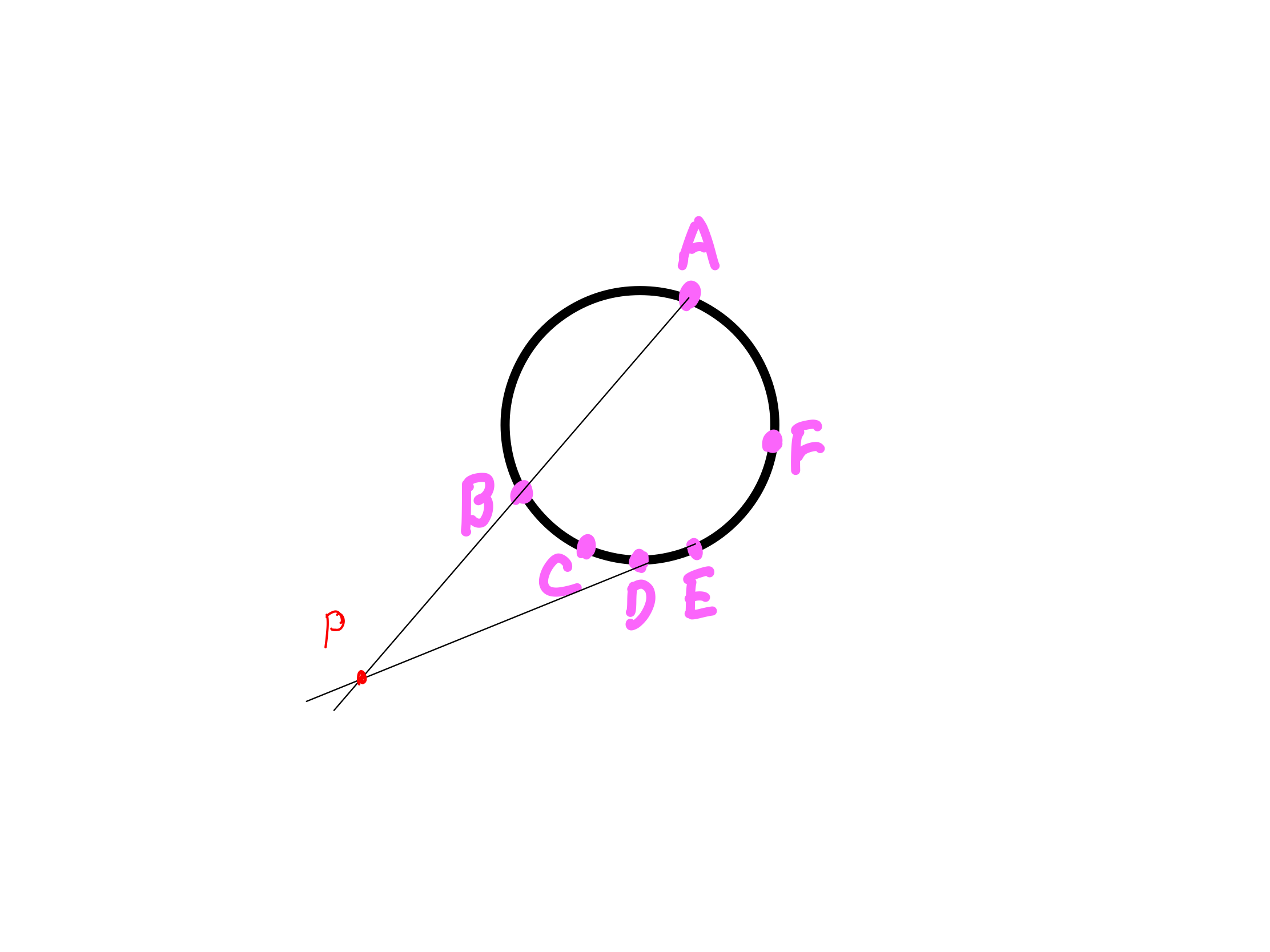
4・線BCと線EFを伸ばして、交わるところを点Qとする
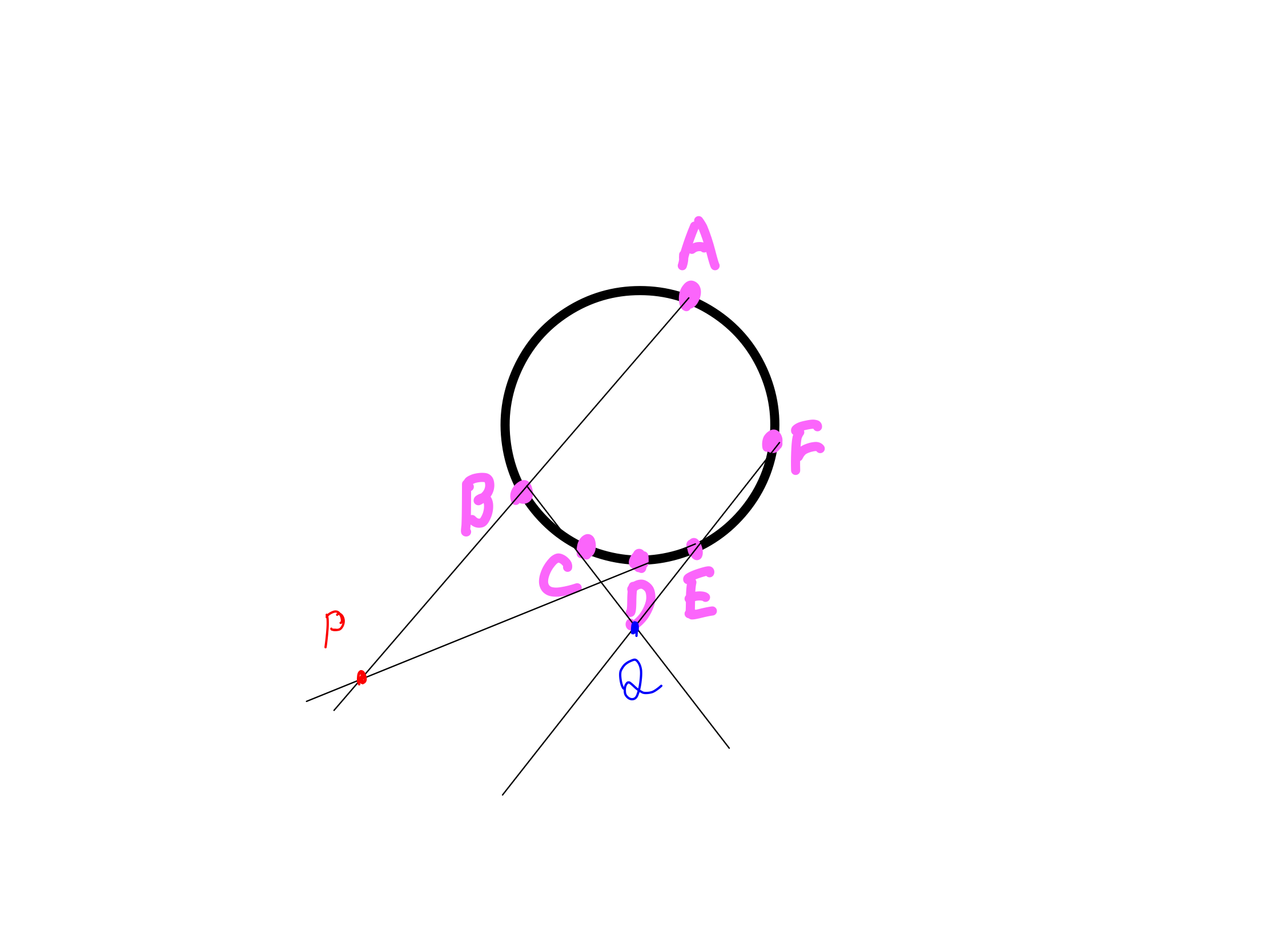
5・線CDと線AFを延長して、交差するところを点Rとする
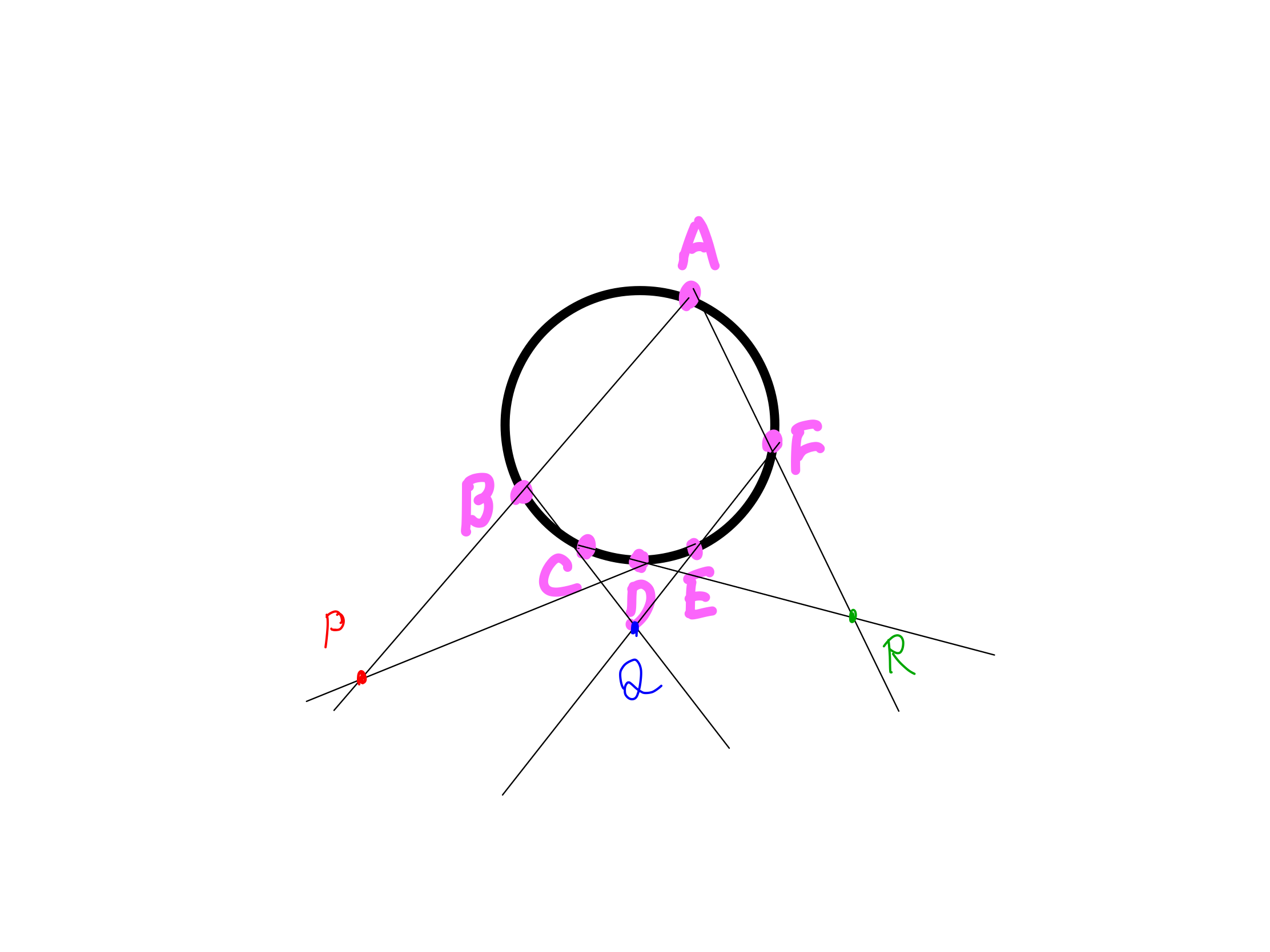
後は、この点P・Q・Rを結ぶと……
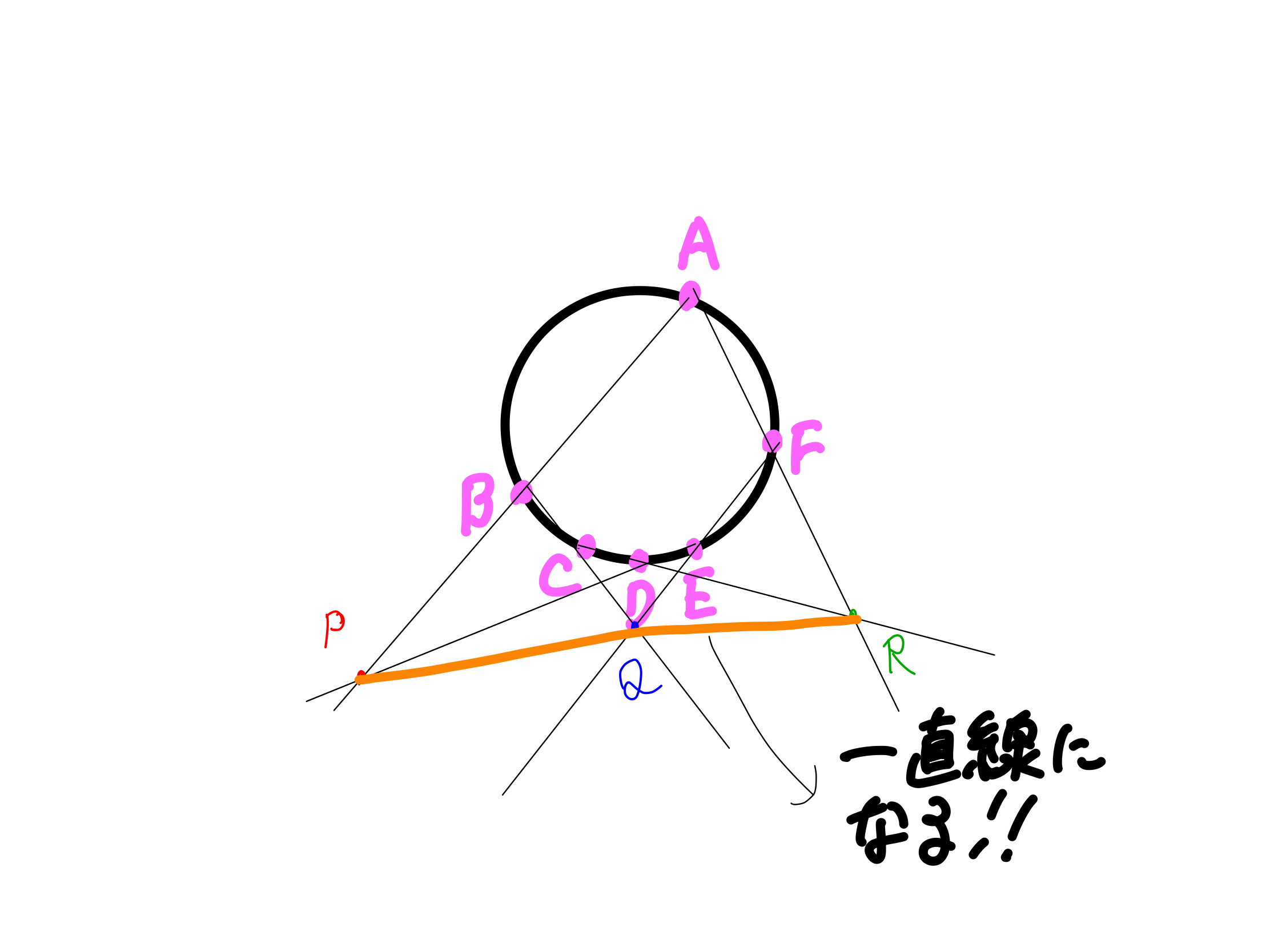
ね、一直線になったでしょ?私、これを実際にやってみたとき「すげぇ!」ってなりましたよ。同時に「でも何の役に立つんだろ」ってなりましたけど(笑)
そう、これが「円に内接する六角形ABCDEFの底辺を延長した直線の交点をP、Q、Rとするとその3点が一直線上になる」ってことなんですよ。やってみると意外と単純でしょう。
さて、次はちょっと違うバージョンでやってみましょう。

コンティニューしてでも理解して!パスカルの定理パート2!
1・円を書く

2・こういう風に点を6つ打つ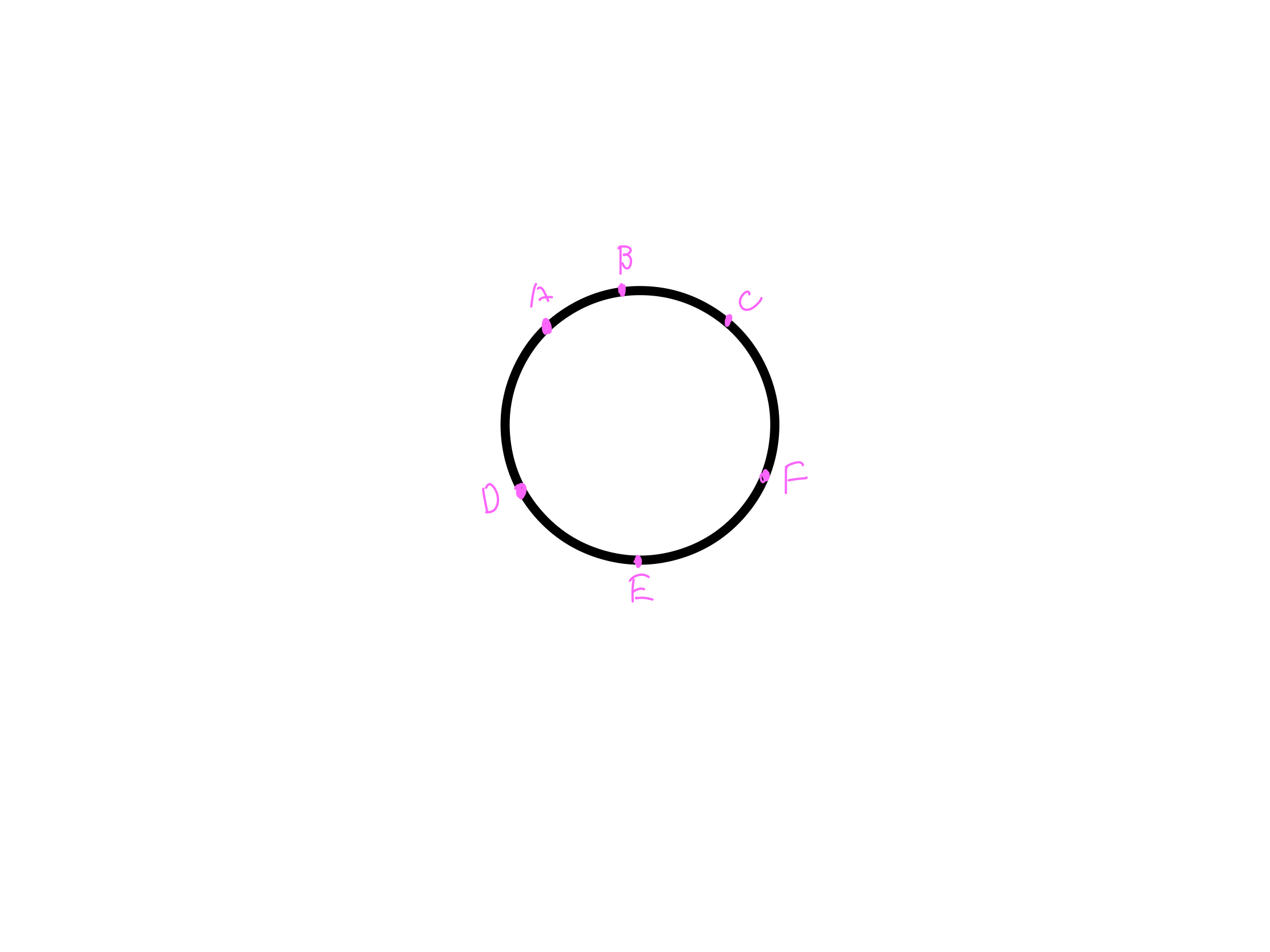
3・線AEとBDにこういう風に書いて、交わるところを点Pとする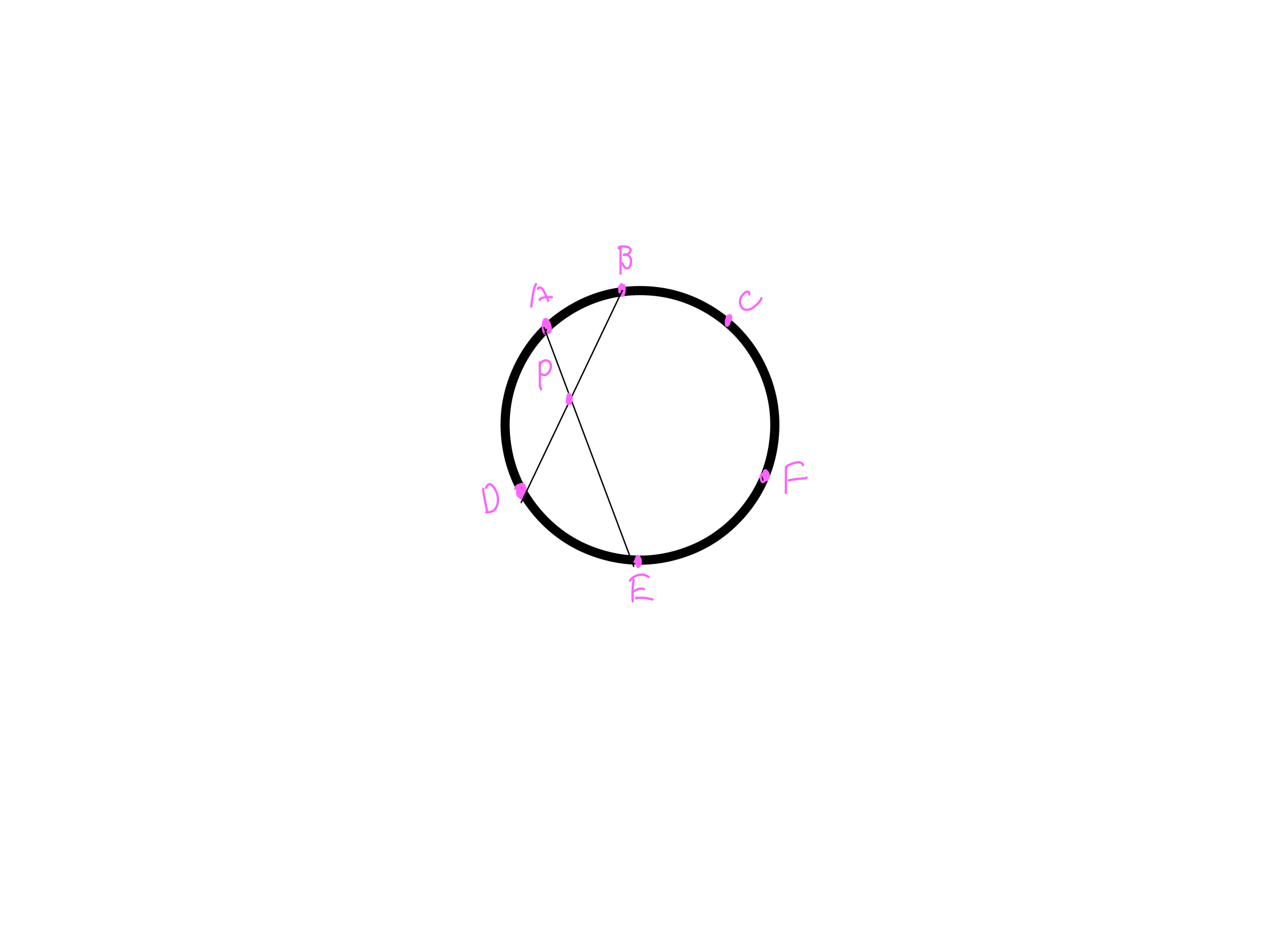
4・線CDとAFに同じような線を引いて、交差するところを点Qとする
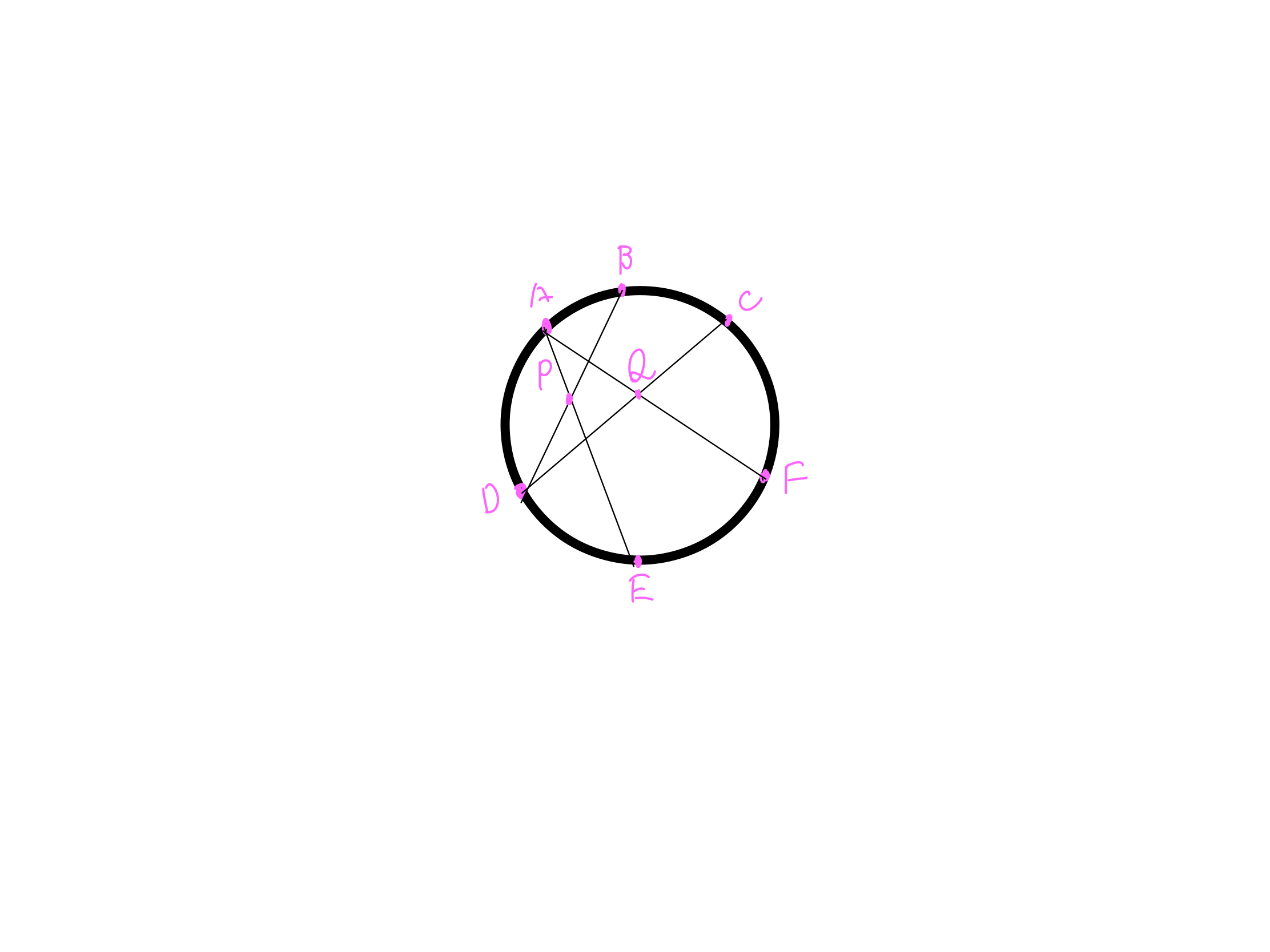
5・線BFとCEも同じようにして、ぶつかるところを点Rとする
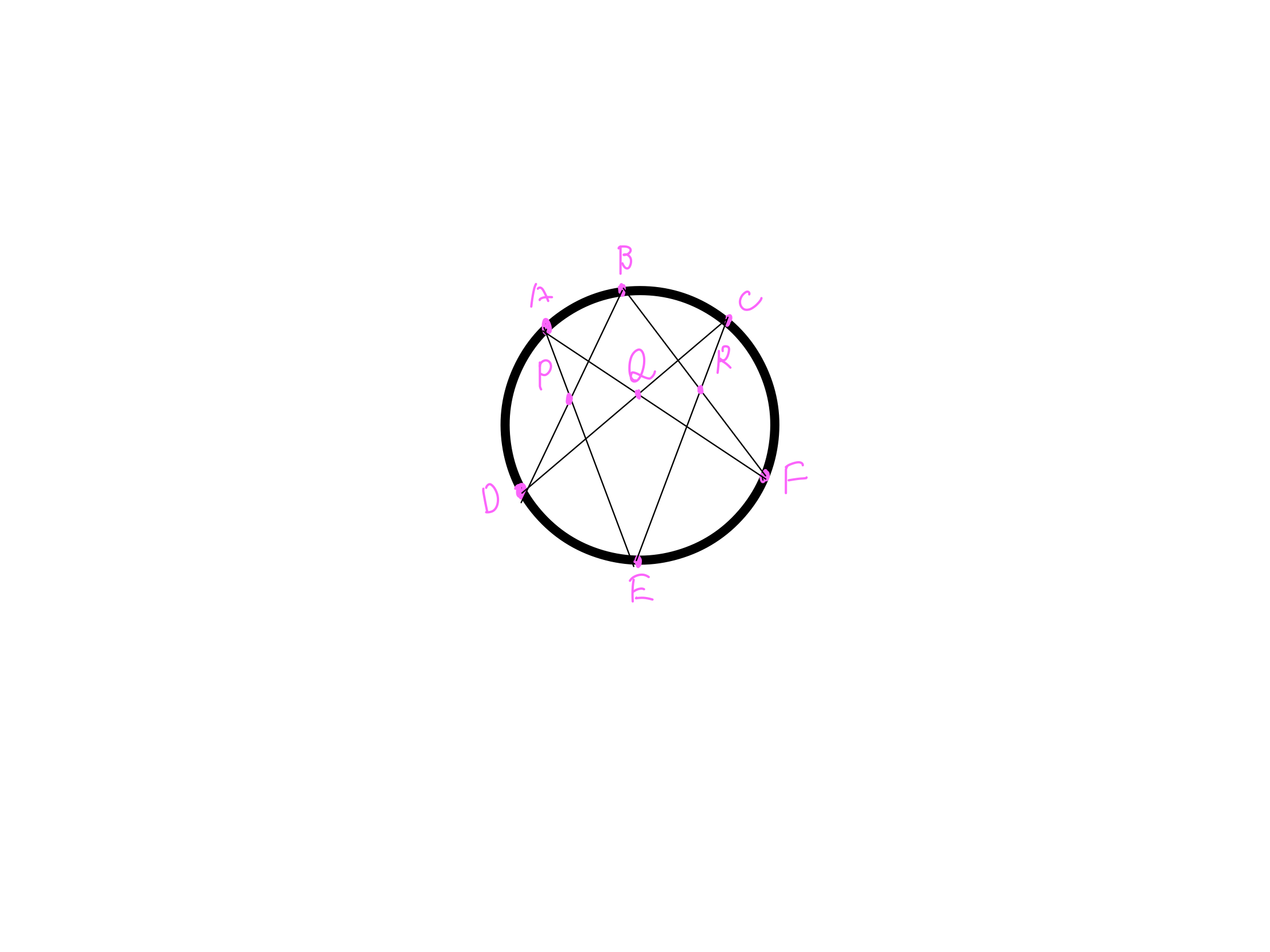
後は点P・Q・Rを結ぶと、
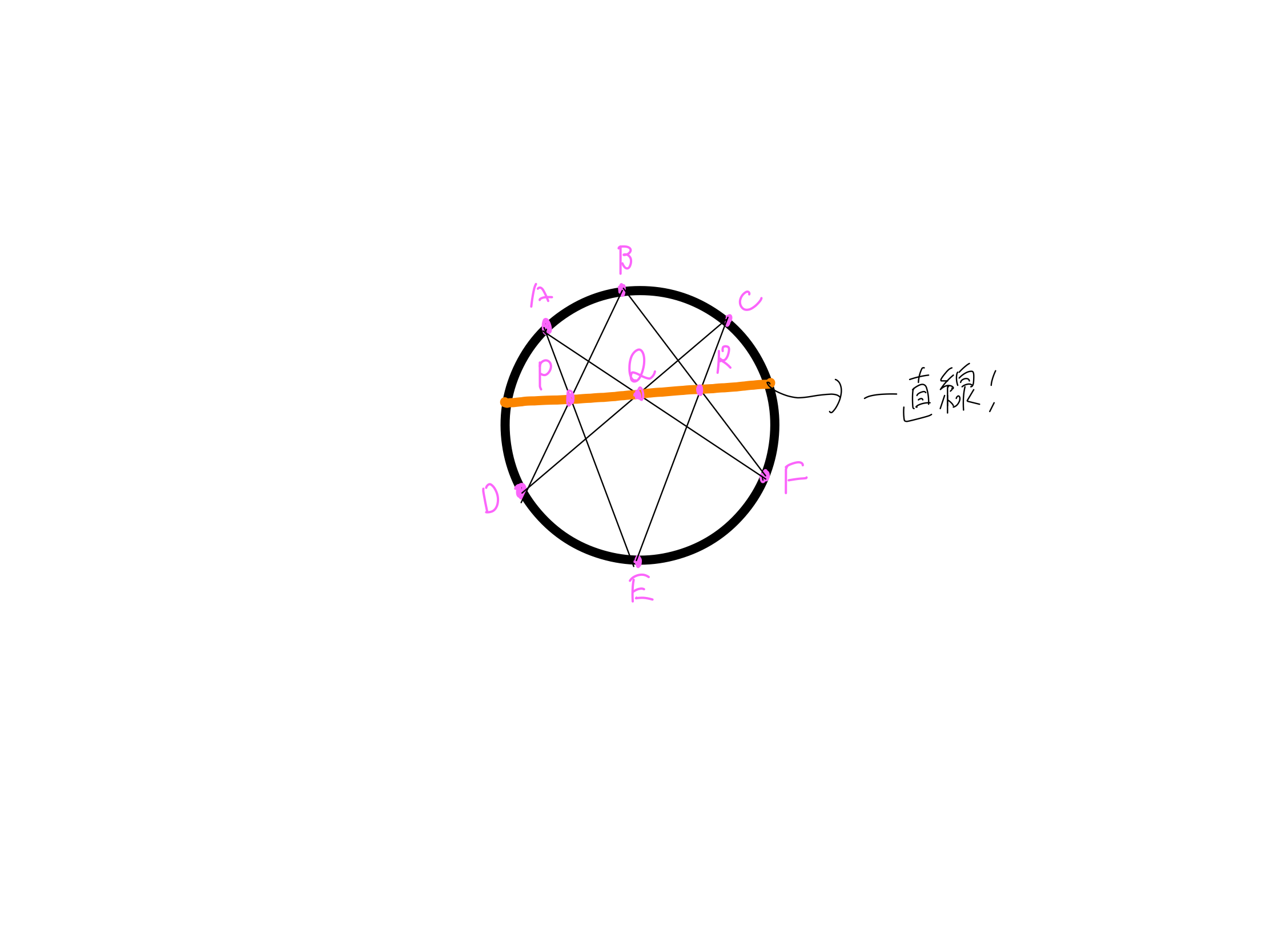
一直線になります。そう、内側にやっても一直線になるのです。
因みにパスカルはこれを神秘的六芒星と呼んでいました。
恐らく内側にやった時の形がユダヤ教のシンボル六芒星(下の図)に似ており、適当に6つ点を打っても一直線という不思議さを神秘的と表現したかったのだと思います。

(ユダヤ教の六芒星。ダビデの星とも呼ばれており、余談だがナチスがユダヤ人を迫害するときに見分けがつくようにユダヤ人の胸に六芒星のワッペンを貼らせたことがある)

……「ねぇよ、そんなもん」という冷めた視線を向けられた気がしますが、気のせいだと思っておきましょう。
(語感良いじゃん……神秘的六芒星……ニートンさんなら分かってくれますよね!)

パスカルの定理のエピソード
このパスカルの定理、いつ見つけられたのか。冒頭で言った通り、パスカルが16歳の時です。16歳ですよ、16歳。現代日本では高校1年生。ぴっかぴっかの(高校)1年生です。
しかもパスカルはこれを1ページにまとめて発表したんです。
この僅か1ページの論文がパスカルの名声を大きく上げることになるんです。(同時に虚栄心の錨を深く下ろすことにもなるのですが、それはまた別のお話)
褒めたのか貶したのか。そこが問題だ。
~デカルトの評価は如何に?~
さて、この論文。実はあのデカルトも目にしているのです。幾何学者としても名高いデカルトはどう評価したのでしょうか。実は本によって書かれている事が違うんです。
『数学物語』という本の中では、
「とても16歳が書いたとは思えない」
と高評価を下しています。しかし、また別のある本では
「デザルク(パスカルの前にこれと似たようなことをした人)の二番煎じ」(意訳)
と評しています。私が今まで見た本の中では後者の方が多かったので、そうだと思うのですが……皆さんはどっちだと思います?
次はサイクロイドについての説明ですね!いっきましょー!

サイクロイド問題(またの名をおにぎり転がす問題)
サイクロイド。サイクロンを彷彿させるのですが、これはいったいどういうものなのでしょうか。本を見ると、こう書いてありました。

「あー!見たことあるー!」「受験でやったー!」となる人がいるのではないでしょうか。

「いいか?丸だと思うから解けなくなるんだ!おにぎり転がす問題だと思えば解ける!」
と言っていましたが、おにぎりに気を取られすぎて肝心の解説を聞き逃してしまいました。先生、すみません。
サイクロイドはルーレット?ルーレットはパスカルが作った言葉?
実はパスカルはサイクロイドとは呼んでいないんですね。なんと呼んでいるか。ルーレットと呼んでいるのです。
ルーレットというとギャンブルでよく使うアレを想像するでしょう。


さらに加えていえば、ルーレットと共にある賭け金を置くテーブル(下の図)、

これもパスカルの発明らしいです。どこまで天才なんでしょう、この人。
さて、サイクロイドについて研究していたパスカルはとある事件を起こしているのです。
サイクロイド事件~コンテスト開いたけど正解者が出ず結局自分を優勝とした!?~
パスカルがサイクロイドを研究し始めたのは1654年でした。思想のページでも説明しましたが、この頃パスカルは回心(宗教に入り込むことを)し、科学からは離れていました。
ところがある日のことです。
あまりにも歯痛が酷くなり、サイクロイドの研究に取り組みました。すると、その痛みがすうっと引きました。そこからパスカルは「神様は僕に研究をしていいってことなんだ!」と解釈し、この研究に熱を上げるようになったのです。
1658年、パスカルは周りの貴族の庇護を得て、サイクロイドの問題をテーマにした数学コンテストを開きました。優勝者には賞金が出る仕組みになっていたほど、しっかりしていたようです。
しかし、何故宗教に傾いて理性を捨てたはずのパスカルがコンテストを開いたのか?
実はこの少し前、パスカルは『キリスト教護教論』─後に『パンセ』となる、いや『パンセ』となってしまう書物の執筆に取り掛かります。
『キリスト教護教論』を出す前にみんなが見てくれるようにセンセーションをぶち込んでおくために行なったのではないか。そう考えられています。
さて、コンテストを開いたは良いものの、色んな事情で問題が変わっていきます。コンテストに参加していた数学者の多くがこの状況を見て、参加を取りやめました。
結局答えをパスカルに送ってきたのはイギリス人数学者2人でした。パスカルはその答えに満足しませんでした。しかし、優勝者を決めなければコンテストの体が成り立たない。
非常に困っていたそんな時にA・デトンヴィルという数学者から完璧な解答が送られてきました。勿論デトンヴィルは堂々の優勝、こうしてコンテストは晴れて幕引き……
─というわけにはいきませんでした。貴族達はパスカルにクレームを付けました。何故か?当然のことです。
そもそもA・デトンヴィルという人物は存在しないのですから。
A・デトンヴィルとは、パスカルが『キリスト教護教論』を出す際につける予定のルイ・ド・モンタルトのアナグラムでした。
ハンドルネームのハンドルネーム─主催者パスカル本人だということがバレたのです。
このバチが当たったのでしょうか。
パスカルは『キリスト教護教論』を完成させる前に亡くなり、非常に不可解な書物『パンセ』として世に出され、元々の目的も達成できずに終わりました。


結論 パスカルは天才だけど色々大変
さて、まとめましょう。
- デカルトすら嫉妬させた(?)パスカルの定理(神秘的六芒星)
- 自分で開いたコンテストなのに優勝者が居ず、結局自分を優勝としてしまったサイクロイド問題(ルーレット問題)
です。



……「気持ち悪い」って声が聞こえた気がしますが、気のせいでしょう。

パスカルの参考文献の紹介です。
参考文献
1・100分de名著 パスカル パンセ

1回25分、全4回で世界の名著を解説していくNHKの番組『100分de名著』のテキスト。入門書だけどかなり詳しく書いてあって、記事を書くときに何度も助けられた。
これからズラーっと参考文献を提示していくけど「こんなに読めねぇよ!」って人はもうこれ1冊だけ読んで。パスカルは大体語れるようになる。
2・『数学の歴史物語』

テレビの人気司会者が書いた数学解説本。数学者達のエピソードやその業績を面白い語り口で説明してくれる文系には嬉しい本。一回騙されたと思って読んでみてほしい。
3・100人の数学者

色んな数学者のエピソードと業績が少しずつ書いてある本。数学セミナーってあるけど文系にも優しかった。
4・『数学の歴史 3』

タイトル通り数学の歴史について綴ってある文章。新装版と書いてあるけど、いささかフォントが昭和っぽい。でもきちんとしている本。









哲学にまつわる小説を書いてらっしゃる白兎扇一〈@WhiteRabbit1900〉さんに書いて頂きました